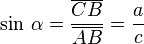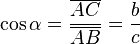2. DEFINICIÓN:
- SEN a
- COS a
- TG a
4. BIOGRAFÍA DE PTOLOMEO
1.
El origen de la palabra TRIGONOMETRÍA proviene del griego "trígonos" (triángulo) y "metros" (metria).Los
babilonios y los egipcios (hace más de 3000 años) fueron los primeros
en utilizar los ángulos de un triángulo y las razones trigonométricas
para efectuar medidas en agricultura y para construir pirámides.
Posteriormente se desarrolló más con el estudio de la astronomía
mediante la predicción de las rutas y posiciones de los cuerpos celestes
y para mejorar la exactitud en la navegación y en el cálculo del tiempo
y los calendarios.
El estudio de la trigonometría pasó
después a Grecia, donde destaca el matemático y astrónomo Griego Hiparco
de Nicea. Más tarde se difundió por India y Arabia donde era utilizada
en la Astronomía. Desde Arabia se extendió por Europa, donde finalmente
se separa de la Astronomía para convertirse en una rama independiente de
las Matemáticas.
A
finales del siglo VIII los astrónomos Árabes trabajaron con la función
seno y a finales del siglo X ya habían completado la función seno y las
otras cinco funciones. También descubrieron y demostraron teoremas
fundamentales de la trigonometría.
A principios del siglo XVII, el matemático John Napier inventó los logaritmos y gracias a esto los cálculos trigonométricos recibieron un gran empuje.
A
mediados del siglo XVII Newton encontró la serie para el sen x y series
similares para el cos x y la tg x. Con la invención del cálculo las
funciones trigonométricas fueron incorporadas al análisis, donde todavía
hoy desempeñan un importante papel tanto en las matemáticas puras como
en las aplicadas.
Por
último, en el siglo XVIII, el matemático Leonhard Euler demostró que
las propiedades de la trigonometría eran producto de la aritmética de
los números complejos y además definió las funciones trigonométricas
utilizando expresiones con exponenciales de números complejos.
2.
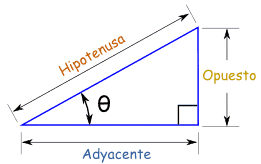
- El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.
- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
3.
1-
1-
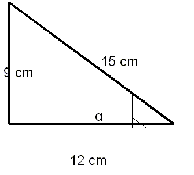
Como ves, los tres lados del triángulo son conocidos, así
que para calcular las razones trigonométricas sólo tenemos que aplicar las
fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y
la hipotenusa 15.
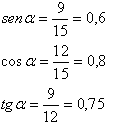
2-
torre,
el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio
a una altura de 1,5 m:
Para comenzar, vamos a hacer un dibujo
que
aclare un poco la situación poniendo los datos que conocemos.
que
aclare un poco la situación poniendo los datos que conocemos.
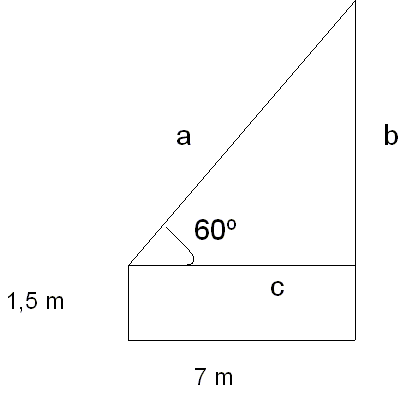
Si nos fijamos en el triángulo, el lado c mide 7 m y
una vez que tengamos calculado el lado b, para calcular la altura de la torre
sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.
Para el ángulo 60º, el lado que conozco es el
cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo
la tangente de 60º.
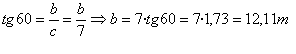
Por tanto la altura de la torre es 12,11 m + 1,5
m = 13, 61 m.
3-
Sabiendo que cos 42º = 0,74. Calcula:sen 222º, tg
138º, cos 48º, sen 318º y sen 132º:
sen 222º
El ángulo 222º pertenece al tercer cuadrante.
Vamos a ver con que ángulo del primero se relaciona: α = 222º - 180º = 42º.
Por tanto y teniendo en cuenta que el seno en el tercer cuadrante es negativo, sen222º = - sen 42º = - 0,669
Por tanto y teniendo en cuenta que el seno en el tercer cuadrante es negativo, sen222º = - sen 42º = - 0,669
tg 138º
138º está en el segundo cuadrante y se relaciona
del primero con α = 180º - 138º = 42º, que vuelve a ser el ángulo que conocemos.
Como la tangente es negativa en el segundo cuadrante, tg 138º= - tg 42º= -0,9
Como la tangente es negativa en el segundo cuadrante, tg 138º= - tg 42º= -0,9
cos 48º
48º es del primer cuadrante, pero cumple que es
el complementario del ángulo que conozco 42º.
Entonces cos 48º = sen 42º = 0,669.
Entonces cos 48º = sen 42º = 0,669.
sen 318º
318º está en el cuarto cuadrante y se relaciona
con 360º - 318º = 42.
Entonces sen 318 º= - sen 42º = - 0,669
Entonces sen 318 º= - sen 42º = - 0,669
sen132º
132º es del segundo y se relaciona con 180º - 132º =
48º que es el complementario de 42º.
Entonces y como el seno es positivo en el segundo cuadrante, sen 132º = sen 48º = cos 42º = 0,74.
Entonces y como el seno es positivo en el segundo cuadrante, sen 132º = sen 48º = cos 42º = 0,74.
4.
(O Ptolomeo; Siglo II) Astrónomo, matemático y
geógrafo griego. Es muy poca la información sobre la vida de Tolomeo que
ha llegado hasta nuestro tiempo. No se sabe con exactitud dónde nació,
aunque se supone que fue en Egipto, ni tampoco dónde falleció.
Su actividad se enmarca entre las fechas de su primera
observación, cuya realización asignó al undécimo año del reinado de
Adriano (127 d.C.), y de la última, fechada en el 141 d.C. En su
catálogo de estrellas, adoptó el primer año del reinado de Antonino Pío
(138 a.C.) como fecha de referencia para las coordenadas.
Tolomeo
fue el último gran representante de la astronomía griega y, según la
tradición, desarrolló su actividad de observador en el templo de Serapis
en Canopus, cerca de Alejandría. Su obra principal y más famosa, que
influyó en la astronomía árabe y europea hasta el Renacimiento, es la Sintaxis matemática,
en trece volúmenes, que en griego fue calificada de grande o extensa
(megalé) para distinguirla de otra colección de textos astronómicos
debidos a diversos autores.
La admiración inspirada por la obra de Tolomeo introdujo la costumbre de referirse a ella utilizando el término griego megisté
(la grandísima, la máxima); el califa al-Mamun la hizo traducir al
árabe en el año 827, y del nombre de al-Magisti que tomó dicha
traducción procede el título de Almagesto adoptado generalmente
en el Occidente medieval a partir de la primera traducción de la versión
árabe, realizada en Toledo en 1175.
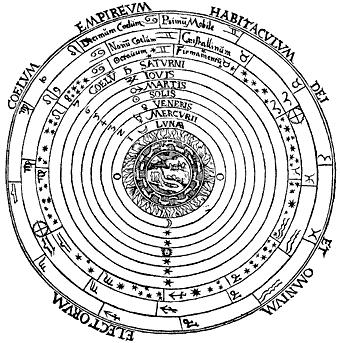
Utilizando los
datos recogidos por sus predecesores, especialmente por Hiparco, Tolomeo
construyó un sistema del mundo que representaba con un grado de
precisión satisfactoria los movimientos aparentes del Sol, la Luna y los
cinco planetas entonces conocidos, mediante recursos geométricos y
calculísticos de considerable complejidad; se trata de un sistema
geocéntrico según el cual la Tierra se encuentra inmóvil en el centro
del universo, mientras que en torno a ella giran, en orden creciente de
distancia, la Luna, Mercurio, Venus, el Sol, Marte, Júpiter y Saturno.
El universo geocéntrico de Tolomeo
Con todo, la Tierra ocupa una posición ligeramente
excéntrica respecto del centro de las circunferencias sobre las que se
mueven los demás cuerpos celestes, llamadas círculos deferentes. Además,
únicamente el Sol recorre su deferente con movimiento uniforme,
mientras que la Luna y los planetas se mueven sobre otro círculo,
llamado epiciclo, cuyo centro gira sobre el deferente y permite explicar
las irregularidades observadas en el movimiento de dichos cuerpos.
El
sistema de Tolomeo proporcionó una interpretación cinemática de los
movimientos planetarios que encajó bien con los principios de la
cosmología aristotélica, y se mantuvo como único modelo del mundo hasta
el Renacimiento, aun cuando la mayor precisión alcanzada en las
observaciones astronómicas a finales del período medieval hizo necesaria
la introducción de decenas de nuevos epiciclos, con lo cual resultó un
sistema excesivamente complicado y farragoso.
